小学生の図形を書く能力が素晴らしいと感じている中村です、こんにちは。（上の画像ですが、実際に小学生が書いたものです。）

さて、前回（その1）の記事では、主に直感的思考を右脳が担当、論理的思考を左脳が担当することを紹介しました（まだその1を読んでいない方はお手数ですが画面を下にスクロールしてその1からお読み下さい）。

右脳…イメージ・芸術性・創造性・ひらめき・空間認識に関係しやすい（直感的思考）

左脳…計算・言語・記憶・分析に関係しやすい（論理的思考）

 そして小学生の間は、不足しやすい「右脳のトレーニング」を意識してするのが良いと言いました。今回の記事ではなぜ私がそう考えているのかを説明してまいります。

 一般的に小学生で学習する算数は計算・文章題・公式を使って面積を出したり速さを求めたりすることです。これらは右脳・左脳どちらを鍛えるものでしょうか。

 計算の学習はたし算・ひき算から始まり分数や小数のかけ算・わり算までします。計算の学習ですから、鍛えれられるのは主に左脳になります。

 文章題はどうでしょうか。「駅まで5kmあり、そのうち3km進みました。残りの距離は何kmですか。」という問題であれば問題文を読み（言語を扱い）、「5kmのうち3km進んだから残りを求めるには5－3＝2（km）」と論理的に考えて式を作り、答えを求めます。これも左脳になりますね。

 「たて5㎝、横4㎝の長方形の面積を求めなさい。」という問題はどちらでしょうか。最初は1辺1㎝の正方形がいくつ入るかを図的に考えますが、最終的には覚えている公式に当てはめて（記憶）、「5×4＝20（㎠）」と計算します。やっぱり左脳ですね。

 「時速30kmで2時間移動しました。移動距離は何kmですか。」という速さについての問題はどうでしょう。「1時間に30km移動する速さで2時間ということは、時間が2倍になっているな。ということは移動距離も2倍で60km移動することになる。」と論理的に考えて答えを出します。またもや左脳です。

 もうおわかりですね。小学生の算数では右脳を鍛えるような学習をあまりしないことになっているのです。もちろん右脳を鍛える単元もあります。以下の問題はどうでしょうか。

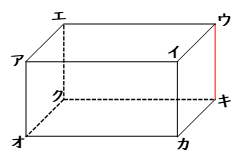
問題：上の図は直方体の見取図です。辺ウキに平行になっている辺はどれですか。

答え：辺イカ、辺アオ、辺エク

 空間認識に関係する問題ですから、これは右脳を鍛えてくれます。しかし、小学生では計算や文章題を学習することがかなりの割合を占めています。右脳と左脳をバランス良く鍛えたいものですが、普通に学習しているだけでは右脳を鍛えることが足りなくなるのです。

 そして脳の発達の大部分を終えた中学生以降で、より右脳を使う問題に直面します。放物線と直線が座標平面上で交わっているグラフ上の三角形の面積を求める問題（1次関数と2次関数の融合問題）や、立体図形の中で三平方の定理を使って長さを求める問題は入試でもよく見ますが、解くことに多くの生徒が苦労します。

「直線と放物線が交わった点と原点で作る三角形の面積を求めるには…？？？」「直方体を頂点を通る平面で切断して切断面の長方形に対角線を引くと直角三角形ができる…のか？？？」

脳の成長がほぼ終わりを迎えた中学生以降で右脳を使った思考力を鍛えることは難しいです。全く意味が無いとは言いませんが、脳が成長途中であるうちに鍛えるのとは効果が違います。

 ではどうすれば良いのでしょうか。やはり小学生のうちに…（その3へつづく）