あの頃は若かった中村です。こんにちは。イライラ経験シリーズその3として、今回は流動性推理についての失敗例を紹介します。

数学の個別指導授業で中1生の方程式を教えていた時でした。生徒から質問がありました。

生徒「先生、x/3＝5の問題わかりません。」

中村「（/3のところを指し示して）これって÷3されているのが邪魔だよね。÷3の逆は×3だから両辺を3倍してｘ＝15だ。わかった？」

生徒「わかりました。」

このように説明してつづきの問題演習を進めていきました。「ｘ/2＝－6」の問題を解いているのを見ると、手が止まっていました。両辺を2倍すれば良いことがわからないようです。

中村「その問題の解き方だけど、（/2のところを指し示して）この部分が邪魔だよね。さっき説明したのと同じやり方になるからやってみて。」

生徒「はい。」

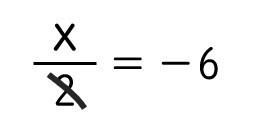
見ると、「ｘ/2＝－6」の分母の部分に斜線を入れて消していったのです。私は（お、両辺2倍して分母消しているな…）と思いつつ見ていると、「ｘ＝－3」と解を求めたのでした。

中村「ちょっとさー、両辺2倍だよねー、何で2で割ってんの？ｘ/2を2で割ってもｘ/4にしかならないのわかるでしょ。両辺2倍してｘ＝－12でしょ（イライラ）。」

生徒「・・・」

ごめんなさい。この指導はダメですね。教え方も下手ですし、イライラしているのもダメです。ではここで確認しましょう。今回のテーマは脳の機能「流動性推理」です。

流動性推理とは

脳の機能の1つで、新しい情報や問題に対して論理的に推論して解決策を見つけるものです。この機能が強いと図形やパターンの規則性を見抜いて欠けている部分を予測することが得意になります。逆に弱いと答えを見つけるための考えが浮かびにくくなります。そのため試行錯誤をすることが苦手になり、同じような間違いを繰り返しやすくなります。

今ではわかります。流動性推理の機能が弱いと両辺を2で割るとどうなるのかをイメージするのが難しいです。そのような生徒にどうなるのか「わかるでしょ。」と当然のように言ってもそれは無理を強いているだけです。

今ではわかります。方程式の計算問題では、最後にｘについている係数で両辺を割って解を求めるパターン（3ｘ＝6だと両辺を3で割ってｘ＝2とするパターン）が多いので、何となく邪魔な2を消しつつ右辺も2で割って「ｘ＝－3」としたことを。

今なら（生徒の理解力と状態に応じて）両辺を2で割るとどうなるのか、2をかけるとどうなるのかを説明します。割ったり掛けたりするパターンを練習して慣れるようにします。そして「違いがわかったみたいだね。ナイス！」と誉めます。

いかがでしたか？こんな失敗談その3でした。ではまた！