（今回の記事はその2からのつづきとなっています。まだ読んでいない方は下にスクロールしてその2からお読みください。）

脳の成長がほぼ終わりを迎えた中学生以降で右脳を使った思考力を鍛えることは難しいです。全く意味が無いとは言いませんが、脳が成長途中である小学生のうちに鍛えるのとは効果が違います。

 ではどうすれば良いのでしょうか。やはり小学生のうちに意識的に右脳向けの問題を解くことです。例えばコメットセミナーでは以下の問題を解きます。

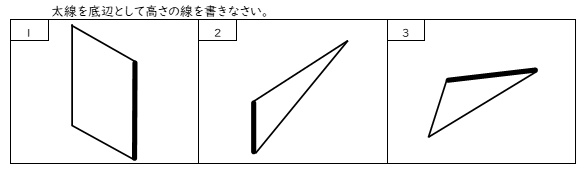
答えを書く時ですが、底辺と高さは垂直の関係になっていることがポイントです。1番の問題は平行四辺形内に線を書くものなので、難しくありません。でも線自体は真横に引かなければなりません。2番や3番は頂点から底辺へ垂線を下ろすのですが、その線が三角形の外に出るようになり、テキトウに引くと上手く書けないようになっています。

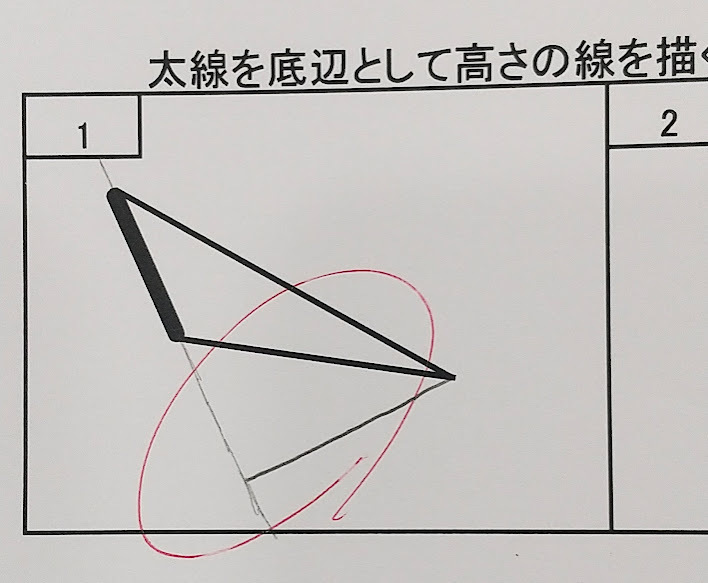
実際に生徒にこの問題を出すと、底辺に対して斜めになった線（垂直にならない線）を書くことがほとんどです。そこで「垂直の関係になっているということはこことここが同じ角度で90度になる必要があって…」と説明します。さらに「これくらいの角度にするとちょうど90度になるね」と見本を見せて、解き直しをします。こうすることで位置・向き・角度の感覚が鍛えられるのです。

 上の画像ですが、実際に生徒が書いた垂線です。最初は斜めになった線を書いていたのですが、書いた結果を見て（ここが角度小さいな…）などと考えつつ線を消す→角度を調整して書き直す→ほぼ完ぺきな垂直な線が完成、となったのでした。

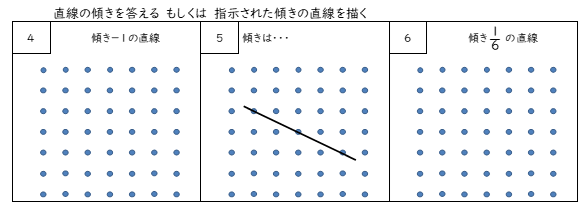
この問題をどう思いますか？

小学生では基本的に負の数（マイナスの数）を扱いません。しかし何マス右に進んで何マス上に進んだ（下に下がった）線なのかは判断できますので、1次関数の直線がどのようになるかを教えることは十分できます。数値を傾きのある直線になおすことと、その逆に直線の傾き具合を数値に直すことは右脳・左脳両方の思考を繋ぐためのトレーニングになりお勧めです。

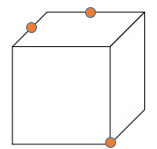
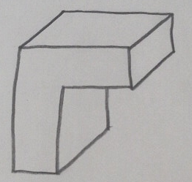
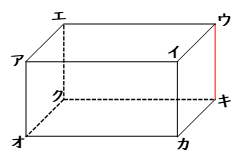
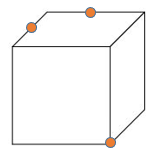
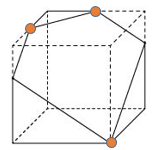
問題：上の立方体を●のついた3点を通る平面で切断します。切り口の形は何になりますか。

 この問題はみなさんにも考えていただきましょう。さぁ、答えを考えてみて下さい！

・

・

・

・

・

 では答えを発表しますね。

 答え：五角形

これらの問題は小学校でトレーニング材料になることは原則ありません。でもそういった問題は小学生にとって普段とはちがった楽しいものであることが多いです。右脳を使うことは直感的にできることであり、感覚が新鮮でもあるのでそうなるのでしょう。

他にも（算数の学習とは離れますが）、サッカーやバスケットボールなどの集団競技をするのは効果的です。自分と相手プレイヤーの位置を把握し、どちらへ自分が動けば良いか、どの方向にパスを出せば効果的かを自然と考えるようになります。

先のブログで紹介したゲーム「立体四目」のように空間を意識しながら勝負を楽しむのも良いです。幼稚園のお子さんに絵本を読み聞かせれば聞いた文章から場面をイメージすることになり、これも良いトレーニングになります（言語理解が進むことで左脳にも良い影響を与えます）。

 いかがでしょうか。このような右脳を鍛えることを是非やっていただきたいです。そしてそれがお子さんの成長に繋がれば嬉しいものです。

参考まで。ではまた！

小学生の図形を書く能力が素晴らしいと感じている中村です、こんにちは。（上の画像ですが、実際に小学生が書いたものです。）

さて、前回（その1）の記事では、主に直感的思考を右脳が担当、論理的思考を左脳が担当することを紹介しました（まだその1を読んでいない方はお手数ですが画面を下にスクロールしてその1からお読み下さい）。

右脳…イメージ・芸術性・創造性・ひらめき・空間認識に関係しやすい（直感的思考）

左脳…計算・言語・記憶・分析に関係しやすい（論理的思考）

 そして小学生の間は、不足しやすい「右脳のトレーニング」を意識してするのが良いと言いました。今回の記事ではなぜ私がそう考えているのかを説明してまいります。

 一般的に小学生で学習する算数は計算・文章題・公式を使って面積を出したり速さを求めたりすることです。これらは右脳・左脳どちらを鍛えるものでしょうか。

 計算の学習はたし算・ひき算から始まり分数や小数のかけ算・わり算までします。計算の学習ですから、鍛えれられるのは主に左脳になります。

 文章題はどうでしょうか。「駅まで5kmあり、そのうち3km進みました。残りの距離は何kmですか。」という問題であれば問題文を読み（言語を扱い）、「5kmのうち3km進んだから残りを求めるには5－3＝2（km）」と論理的に考えて式を作り、答えを求めます。これも左脳になりますね。

 「たて5㎝、横4㎝の長方形の面積を求めなさい。」という問題はどちらでしょうか。最初は1辺1㎝の正方形がいくつ入るかを図的に考えますが、最終的には覚えている公式に当てはめて（記憶）、「5×4＝20（㎠）」と計算します。やっぱり左脳ですね。

 「時速30kmで2時間移動しました。移動距離は何kmですか。」という速さについての問題はどうでしょう。「1時間に30km移動する速さで2時間ということは、時間が2倍になっているな。ということは移動距離も2倍で60km移動することになる。」と論理的に考えて答えを出します。またもや左脳です。

 もうおわかりですね。小学生の算数では右脳を鍛えるような学習をあまりしないことになっているのです。もちろん右脳を鍛える単元もあります。以下の問題はどうでしょうか。

問題：上の図は直方体の見取図です。辺ウキに平行になっている辺はどれですか。

答え：辺イカ、辺アオ、辺エク

 空間認識に関係する問題ですから、これは右脳を鍛えてくれます。しかし、小学生では計算や文章題を学習することがかなりの割合を占めています。右脳と左脳をバランス良く鍛えたいものですが、普通に学習しているだけでは右脳を鍛えることが足りなくなるのです。

 そして脳の発達の大部分を終えた中学生以降で、より右脳を使う問題に直面します。放物線と直線が座標平面上で交わっているグラフ上の三角形の面積を求める問題（1次関数と2次関数の融合問題）や、立体図形の中で三平方の定理を使って長さを求める問題は入試でもよく見ますが、解くことに多くの生徒が苦労します。

「直線と放物線が交わった点と原点で作る三角形の面積を求めるには…？？？」「直方体を頂点を通る平面で切断して切断面の長方形に対角線を引くと直角三角形ができる…のか？？？」

脳の成長がほぼ終わりを迎えた中学生以降で右脳を使った思考力を鍛えることは難しいです。全く意味が無いとは言いませんが、脳が成長途中であるうちに鍛えるのとは効果が違います。

 ではどうすれば良いのでしょうか。やはり小学生のうちに…（その3へつづく）

こんにちは、空間認識力が高めの中村です。今回のブログでは、多くの小学生に当てはまる右脳を鍛える学習について、私の考えをお伝えします。（長くなりますので、その１では右脳と左脳の違いの紹介までの話となっています。）

先日のブログで紹介しましたが、人間の脳は右脳と左脳にわかれていて、例えば空間認識を司るのは右脳であることがわかっています。論理的な思考は左脳が担当します。このような違いがあるのですが、結論から言うと一般的に小学校で算数の学習をすると左脳ばかりが鍛えられやすくなります。右脳を鍛えることが足りなくなりやすいので、小学生の間は意識的に右脳を鍛えると良いです。

こう考えるには理由があります。その説明をしていきたいのですが、まずは右脳と左脳の違いから紹介します。

上の画像にあるとおり、左脳は論理的思考を担当します。算数の学習に関係して言えば、言語・分析・計算などを行うときに左脳を働かせることになります。

「赤いテープが10㎝。白いテープは赤いテープより3㎝長く、青いテープは白いテープより5㎝長い。青いテープの長さは何㎝ですか。」

このような問題は問題文（言語）を読み、答えをどう求めていけば考え（分析）、「10㎝より3cm長い白いテープは10＋3＝13（㎝）だから…」と論理的に考えて（計算して）答えを求めることが通常です。

一方で右脳は直感的思考を担当します。例えば、坂が急なのか緩やかなのかの判断は直感的に行うことが多いでしょう。みなさんは以下の画像の坂をどう判断しますか。

この坂は急だと思った人が多いことでしょう。ここを登ったら疲れそうだな、とか何となく見た感じで急だと思ったなら、右脳を使った判断ということになります。これを「この坂は絵だけど、大体10mすすむと4ｍ高くなるから（分析）、割合は4÷10＝0.4（計算）だな。0.4を百分率に変換すると傾斜率40％だ。車にとって急な坂は危険であり、一般的に高速道路の傾斜率は10％未満だから…」と論理的に考えて（左脳を使って）判断した方もいるかもしれません。ですが、そうしない方がほとんどでしょう。このように右脳は直感的な判断をするときに使われます。

実際には右脳だけ、もしくは左脳だけを使って算数の問題を解くわけではありません。生活している時も両方使いながら、状況によってどちらの脳を優位に働かせているか変わってくるものです。そんな右脳と左脳の違いをまとめると以下の通りです。

右脳…直感的思考を担当。イメージ・芸術性・創造性・ひらめき・空間認識に関係しやすい。

左脳…論理的思考を担当。言語・計算・記憶・分析に関係しやすい。

いかがでしょうか。

ここで話を小学生が算数を学習する状況に戻します。小学校で学習する算数は計算・文章題・公式を使って…

（その２へつづく）

こんにちは、コメットセミナーです。学校の社会の定期テストでは時事問題が出題される場合があります。それに向けて時事問題を作りました。今後月に１回のペースでアップしていく予定です。ぜひご利用下さい。

 

【2025年2月のニュース】

・日本では公営ギャンブル以外の賭博は法律で禁止となっている。ルーレットを回して出た数を正解したら賭けた1万円が2万円になった、正解できなかったので賭けたお金が無くなった、ということをすれば賭け事をやったことになる。違法行為をしたということだ。海外では賭博が合法となっている国があり、海外で運営されているオンラインカジノに日本からアクセスしてプレイすることが実際には出来てしまう。このようにしてオンラインカジノを利用した（違法行為をした）芸人やプロ野球選手が活動を自粛する事態が起こった。

・7日に日本の石破茂（いしば しげる）総理大臣はアメリカのドナルド・トランプ大統領と初めて日米首脳会談を行った。今後も日本とアメリカで安全保障と経済について協力していくことが確認された。

・14日に江藤拓農林水産大臣は、米の価格が高くなっているため、政府が保管している備蓄米21万トンの放出を発表した。たくさんの米が市場に流通するとコメの値段が下がるが、それを意図してのもの。流通の円滑化を目的として備蓄米を放出するのはこれが初めてとなる。

・2月24日で2022年にロシアがウクライナ侵攻を始めて3年が経った。アメリカとロシアで和平に向けての話し合いが行われており、ゼレンスキー大統領はウクライナ抜きの話し合いに警戒している。ちなみにロシアの政治的リーダーはプーチン大統領、ウクライナの政治的リーダーはゼレンスキー大統領である。

・25日に日本維新の会は与党である自民党・公明党と、高校授業料の実質無償化で合意した。これにより2025年度予算案に日本維新の会は賛成することになり、予算成立の見通しとなった。

 

【2025年2月　問題】

以下問題を作りました。復習用に解いてみましょう！答えは問題の下にあります。

1．日本では公営ギャンブル以外の賭博は法律違反となり禁止されています。海外で運営するサイトでは賭博が出来るものがあり、スマホを使うなどして日本からアクセスして○○○○○○○○を利用すること（賭け事をすること）が問題となりました。○○○○○○○○に入るカタカナを答えなさい。

2．日本のある総理大臣とアメリカのある大統領が初めて日米首脳会談を行いました。総理大臣、大統領はそれぞれ誰ですか。

3．ある日本の農産物の値段が高くなっています。5㎏あたりの値段が4000円くらいになり、1年前の2倍近くの値段になりました。値段を下げるために農林水産大臣があるものの放出を発表しました。あるものとは何ですか。

4．24日で侵攻から3年が経ちました。この出来事はどこの国がどこに侵攻したものですか。

5．侵攻から3年が経ちましたが、攻めた国、攻められた国の大統領はそれぞれ誰ですか

6．与党である自民党・公明党は日本維新の会と「○○授業料」の実質無料化で合意しました。「　　　」内に入る語句を答えなさい。

 

【2025年2月　解答】

1．日本では公営ギャンブル以外の賭博は法律違反となり禁止されています。海外で運営するサイトでは賭博が出来るものがあり、スマホを使うなどして日本からアクセスして○○○○○○○○を利用すること（賭け事をすること）が問題となりました。○○○○○○○○に入るカタカナを答えなさい。　オンラインカジノ

2．日本のある総理大臣とアメリカのある大統領が初めて日米首脳会談を行いました。総理大臣、大統領はそれぞれ誰ですか。　石破茂（いしば しげる）、ドナルド・トランプ

3．ある日本の農産物の値段が高くなっています。5㎏あたりの値段が4000円くらいになり、1年前の2倍近くの値段になりました。値段を下げるために農林水産大臣があるものの放出を発表しました。あるものとは何ですか。　備蓄米（びちくまい）

4．24日で侵攻から3年が経ちました。この出来事はどこの国がどこに侵攻したものですか。　ロシア、ウクライナ

5．侵攻から3年が経ちましたが、攻めた国、攻められた国の大統領はそれぞれ誰ですか。　プーチン、ゼレンスキー

6．与党である自民党・公明党は日本維新の会と「○○授業料」の実質無料化で合意しました。「　　　」内に入る語句を答えなさい。　高校授業料

　例えば右側手前には黒の玉が真上に4つ並んでいます。この状態を作った黒プレイヤーが勝ちです。左から2列目には高さ2段目に茶色の玉が奥から手前に向かって一直線に並んでいますね。こうなれば茶プレイヤーの勝ちとなります。

　ではここで皆さんへ問題を出します。上の写真には、実はあと１つ一直線に並んでいるところがあります。それはどこでしょう？

 

・

・

・

・

・

・

 

　答えの発表です！以下の写真をご覧ください。

　赤丸で囲われた部分が右奥へ向かって一段ずつ上がりながら一直線に並んでいます。こうなると茶プレイヤーの勝ちです。

　この盤面の並びは説明用に作ったので一直線に並んでいる所がいくつもあっておかしいですが、実際には勝負が決まると１か所だけ一直線が作られることになります。それまでにいろいろな角度から自分の玉をどのように並べるか考え、相手の玉がどのように並んでいるか注意を払うことになります。これが大いに右脳へ刺激を与え、空間認知力を鍛えるのです。

　そういえば、私自身は小学生になったくらいのとき、おじいちゃんの家へ遊びに行ってこのゲームに出会ったのでした。そしてめっちゃハマり、いとこや親戚のおじさんと勝負を繰り広げたのが懐かしいです。

　だから中学生で出てきた問題で、切断された立体の切り口の形を判断したりねじれの位置関係を見つけたりするものが得意だったのかもしれません。ドライブ好きなのも、車の向きや速度、道の形がどのように変わっていくかを感じならが車を操ることが苦にならないから（むしろそれが楽しいから）なのでしょう。

　いかがでしたか？将来に向けて能力を鍛えてくれるこのゲーム、みなさんも是非お試しあれ。ネットでは2000円しない金額で売ってますからすぐ手に入れられます。（決してアマゾンや楽天の回し者ではございませんｗ）

　ではまた！

 

こんにちは、コメットセミナーの中村です。今回のブログではコメットセミナーで取り入れている学習指導のやり方を紹介します。ご家庭で子どもに勉強を教える機会がある方、参考にしていただけるかと思います。

 具体的に紹介するのは、比例関係が成り立つ時の説明テクニックです。口調を授業モードにしつつ、生徒から質問が来たと仮定して説明していきます。

生徒：先生、この問題の解き方わからないので教えて下さい。

先生：はーい。問題は…「1mで40円の糸があります。この糸を5m買うと何円になりますか。」となっているね…。

 

（※実際に質問が出るのは分数になっていたり、速さがわかっていて移動距離を求めたりする問題ですが、ここでは簡単な問題にしてあります。）

 

～　指導例　～

 

先生：例の技が使えるから、説明するね。

生徒：お願いします！

先生：まず基準だけど1mで40円となっているね。そして、5mで何円になるか探しなさいという問題になっているね。

生徒：はい。

先生：ということは（以下の内容を書いて見せて）、こんな関係だね。

 

1m　で　40円

↓

5m　で　    円

 

先生：そうしたら1m→5mになっている所を見よう。ここって何倍になってる？

生徒：5倍

先生：いいね、5倍だ（×5だ）

 

1m　で　40円

↓ ×5

5m　で　    円

 

先生：長さが「×5」されたということは値段の40円も「×5」しないといけないね。40（円）×5はいくつ？

生徒：200！

先生：正解！だから答えは200円だ。わかった？

生徒：わかりました。

先生：ナイス！！

 

～　指導例　おしまい　～

 いかがでしょうか。このやり方で教えてあげると、速さがわかっていてどれだけ時間をかけると移動距離がどれくらいになるのか、仕事率が何Ｗ（ワット）になるのか…など数学・理科の解説に役立ちます。

 公式にあてはめて答えを出すやり方が必要な場面のあるでしょう。そのやり方が手っ取り早く正解を出す方法でもありますが、理解しやすく公式暗記に頼らなくて済む勉強の仕方に繋がりますので、お勧めの説明方法になっています。

 

つづく

 

こんにちは、コメットセミナーの中村です。今回のブログでは、説明テクニックを使って説明すれば公式暗記に頼らなくてすむことを紹介します。前回のブログでは、以下のように比例関係が成り立つ時の説明テクニックを紹介しました。

 １m　で　40円

↓

５m　で　　円

　片方が5倍になっていたらもう片方も5倍して答えを出すというこのやり方、いかがでしょうか。例えば、「時速50kmの速さで4時間動きつづけると、全部で何km移動しますか。」という問題の解説も同じように出来ます。時速50kmが1時間で50km移動する速さであることを理解していることが前提になりますが、それがわかっていれば…

 1時間で50km移動

↓

4時間で　　km移動

 ということを確認し、1時間が4倍されて4時間になっているので、50kmも4倍して200km移動するということを見つけやすくなります。そして移動距離を出すための公式を覚える必要も無くなるのです。

 多くの小学生は、「何km移動しますか。」と問われると「道のり（距離）＝速さ×時間」という公式を使って答えを出します。手っ取り早く公式に当てはめて答えを出せるのは良いのですが、公式に頼ると速さと時間による移動距離のイメージを持たなくなり内容理解に繋がりません。また、「速さ」の単元では「速さ＝道のり÷時間」「時間＝道のり÷速さ」という公式も出てきますので、それらを混同したら何もできなくなります。

 そのようなことを考えて生徒に勉強を教えている今日この頃です。もちろん、この教え方が絶対のものではありません。他にもいくつか説明の仕方はあり、例えば数直線を使った説明も良いでしょう。そのうちの1つとして、今回の説明テクニックが参考になれば嬉しいです。